Building LCS models with lavaan
In lavaan, models are built with a single block of syntax. Regressions are defined with the tilde ~, variances and covariances with a double tilde ~~, and intercepts with ~ 1. To define the latent variables, we use the special operator =~, which can be read as “measured by” or “manifested as”.
To indicate that a path is fixed, we use an asterisk *. For example, in lx2 ~ 1*lx1, the regression path from lx1 to lx2 is fixed to 1. To name a free parameter, we combine the asterisk * with label(""). For example, X1 ~~ label("merX")*X1 means that the variance of X1 is freely estimated and labeled “merX”. We can use the same label for multiple parameters to impose an equality constraint across them.
If necessary, install lavaan:
install.packages("lavaan")The Univariate LCS model
Single indicator
Obtain the example dataset here: Download LCSdata.txt
We will estimate the following model:
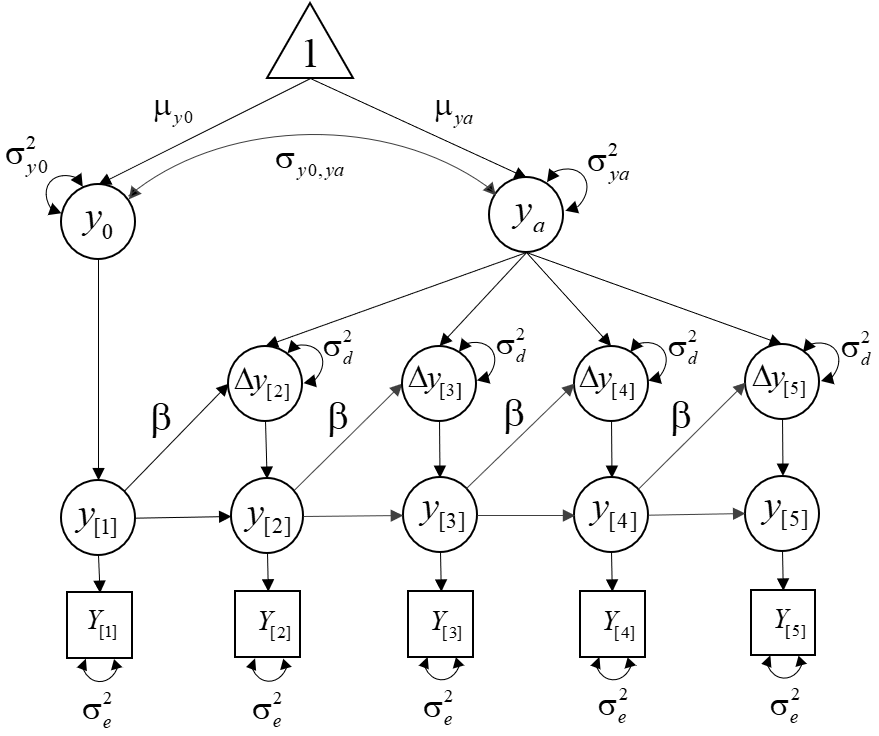
Step 1. Load the package and database:
library(lavaan)
dfwide <- read.table("LCSdata.txt")Step 2. If necessary, name the variables in the database:
Tmax <- 5 # Number of measurement occasions
colnames(dfwide) <- paste0("Y", 1:Tmax)You can use other names for the observed variables, but make sure to use the same names when building the model.
Step 3. Build the model:
LCS.model <- '
### Latent structure
# 1 -> Initial factor and additive component (means)
y0 + ya ~ 1
# (co)variances of the initial factor and additive component
y0 ~~ y0 + ya
ya ~~ ya
# Initial factor -> initial latent score
y0 =~ 1*ly1
# Latent[t-1] -> Latent[t]
ly2 ~ 1*ly1
ly3 ~ 1*ly2
ly4 ~ 1*ly3
ly5 ~ 1*ly4
# Additive component -> Change
ya =~ 1*dy2 + 1*dy3 + 1*dy4 + 1*dy5
# Latent -> Change (self-feedback)
dy2 ~ label("beta")*ly1
dy3 ~ label("beta")*ly2
dy4 ~ label("beta")*ly3
dy5 ~ label("beta")*ly4
# Change -> Latent
dy2 =~ 1*ly2
dy3 =~ 1*ly3
dy4 =~ 1*ly4
dy5 =~ 1*ly5
### Measurement structure
# Latent -> Manifest
ly1 =~ 1*Y1
ly2 =~ 1*Y2
ly3 =~ 1*Y3
ly4 =~ 1*Y4
ly5 =~ 1*Y5
# Measurement error variance
Y1 ~~ label("merY")*Y1
Y2 ~~ label("merY")*Y2
Y3 ~~ label("merY")*Y3
Y4 ~~ label("merY")*Y4
Y5 ~~ label("merY")*Y5
### For the stochastic version of the model, include:
# Dynamic error variance (time-invariant)
dy2 ~~ label("derY")*dy2
dy3 ~~ label("derY")*dy3
dy4 ~~ label("derY")*dy4
dy5 ~~ label("derY")*dy5
'Step 4. Estimate the model parameters:
LCS.fit <- lavaan(LCS.model, data=dfwide)Click here to see the results
summary(LCS.fit, standardized = T)## lavaan 0.6-8 ended normally after 28 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 18
## Number of equality constraints 10
##
## Number of observations 1980
##
## Model Test User Model:
##
## Test statistic 15.123
## Degrees of freedom 12
## P-value (Chi-square) 0.235
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 =~
## ly1 1.000 1.000 1.000
## ya =~
## dy2 1.000 0.696 0.696
## dy3 1.000 0.746 0.746
## dy4 1.000 0.780 0.780
## dy5 1.000 0.801 0.801
## dy2 =~
## ly2 1.000 0.475 0.475
## dy3 =~
## ly3 1.000 0.410 0.410
## dy4 =~
## ly4 1.000 0.365 0.365
## dy5 =~
## ly5 1.000 0.335 0.335
## ly1 =~
## Y1 1.000 0.814 0.847
## ly2 =~
## Y2 1.000 0.859 0.859
## ly3 =~
## Y3 1.000 0.929 0.876
## ly4 =~
## Y4 1.000 0.999 0.890
## ly5 =~
## Y5 1.000 1.059 0.901
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ly2 ~
## ly1 1.000 0.947 0.947
## ly3 ~
## ly2 1.000 0.925 0.925
## ly4 ~
## ly3 1.000 0.930 0.930
## ly5 ~
## ly4 1.000 0.943 0.943
## dy2 ~
## ly1 (beta) -0.240 0.012 -20.455 0.000 -0.478 -0.478
## dy3 ~
## ly2 (beta) -0.240 0.012 -20.455 0.000 -0.541 -0.541
## dy4 ~
## ly3 (beta) -0.240 0.012 -20.455 0.000 -0.611 -0.611
## dy5 ~
## ly4 (beta) -0.240 0.012 -20.455 0.000 -0.675 -0.675
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 ~~
## ya 0.113 0.010 11.064 0.000 0.490 0.490
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 -1.157 0.021 -54.039 0.000 -1.421 -1.421
## ya -0.956 0.025 -37.963 0.000 -3.364 -3.364
## .Y1 0.000 0.000 0.000
## .Y2 0.000 0.000 0.000
## .Y3 0.000 0.000 0.000
## .Y4 0.000 0.000 0.000
## .Y5 0.000 0.000 0.000
## .dy2 0.000 0.000 0.000
## .dy3 0.000 0.000 0.000
## .dy4 0.000 0.000 0.000
## .dy5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 0.662 0.028 23.422 0.000 1.000 1.000
## ya 0.081 0.008 10.727 0.000 1.000 1.000
## .Y1 (merY) 0.261 0.012 21.947 0.000 0.261 0.283
## .Y2 (merY) 0.261 0.012 21.947 0.000 0.261 0.261
## .Y3 (merY) 0.261 0.012 21.947 0.000 0.261 0.232
## .Y4 (merY) 0.261 0.012 21.947 0.000 0.261 0.207
## .Y5 (merY) 0.261 0.012 21.947 0.000 0.261 0.189
## .dy2 (derY) 0.102 0.019 5.374 0.000 0.613 0.613
## .dy3 (derY) 0.102 0.019 5.374 0.000 0.703 0.703
## .dy4 (derY) 0.102 0.019 5.374 0.000 0.768 0.768
## .dy5 (derY) 0.102 0.019 5.374 0.000 0.812 0.812
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000Multiple indicators
Obtain the example dataset here: Download MILCSdata.txt
We will estimate the following model:
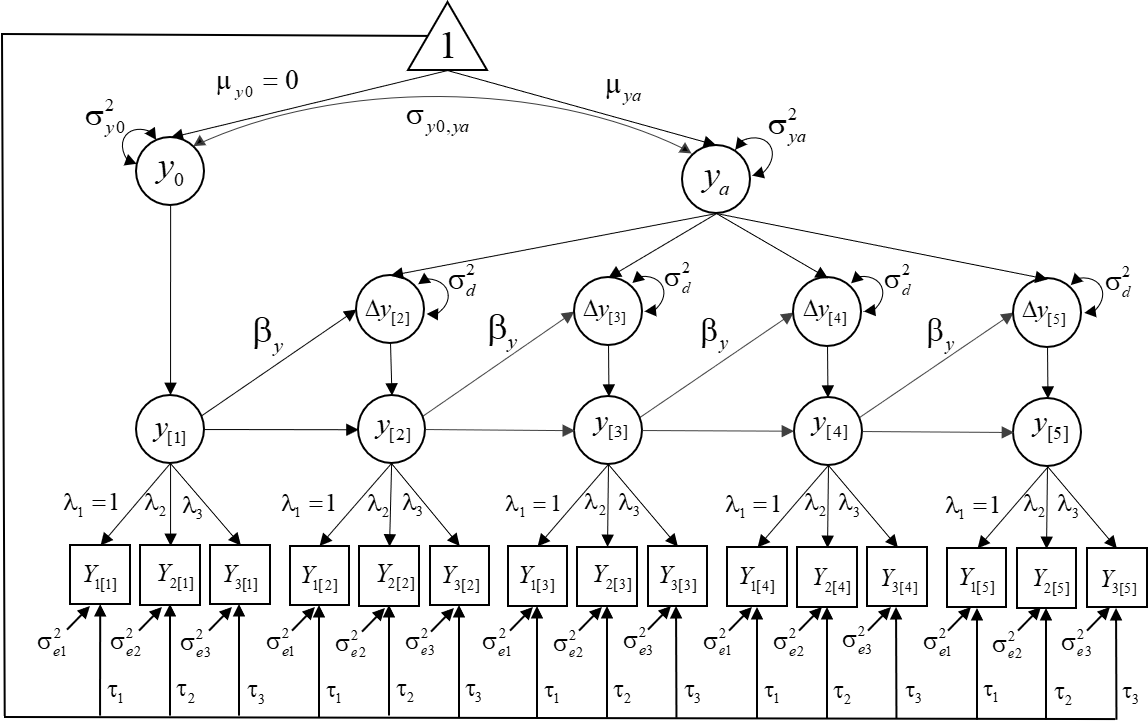
Step 1. Load the package and database:
library(lavaan)
dfwide <- read.table("MILCSdata.txt")Step 2. If necessary, name the variables in the database:
Tmax <- 5 # Number of measurement occasions
n_indic <- 3
colnames(dfwide) <- paste0(rep(paste0("Y", 1:n_indic, "_t"), each=Tmax), 1:Tmax)When building the model, we will refer to the observed variables as Y1_t1, Y2_t1, Y1_t3…, where the first number identifies the indicator and the second identifies the measurement occasion.
Step 3. Build the model:
# 2. Build the model with lavaan code:
MI_LCS.model <- '
### Latent structure
# 1 -> Additive component (mean)
ya ~ 1
# (co)variances of the initial factor and additive component
y0 ~~ y0 + ya
ya ~~ ya
# Initial factor -> First latent score (t=1)
y0 =~ 1*ly1
# Latent[t-1] -> Latent[t]
ly2 ~ 1*ly1
ly3 ~ 1*ly2
ly4 ~ 1*ly3
ly5 ~ 1*ly4
# Additive component -> Change
ya =~ 1*dy2 + 1*dy3 + 1*dy4 + 1*dy5
# Latent -> Change (self-feedback)
dy2 ~ label("beta")*ly1
dy3 ~ label("beta")*ly2
dy4 ~ label("beta")*ly3
dy5 ~ label("beta")*ly4
# Change -> Latent
dy2 =~ 1*ly2
dy3 =~ 1*ly3
dy4 =~ 1*ly4
dy5 =~ 1*ly5
### Measurement structure
# Factor loadings: Configural and weak invariance
ly1 =~ 1*Y1_t1 + label("lambda_Y2")*Y2_t1 + label("lambda_Y3")*Y3_t1
ly2 =~ 1*Y1_t2 + label("lambda_Y2")*Y2_t2 + label("lambda_Y3")*Y3_t2
ly3 =~ 1*Y1_t3 + label("lambda_Y2")*Y2_t3 + label("lambda_Y3")*Y3_t3
ly4 =~ 1*Y1_t4 + label("lambda_Y2")*Y2_t4 + label("lambda_Y3")*Y3_t4
ly5 =~ 1*Y1_t5 + label("lambda_Y2")*Y2_t5 + label("lambda_Y3")*Y3_t5
# Intercepts of the indicators: Strong invariance
Y1_t1 + Y1_t2 + Y1_t3 + Y1_t4 + Y1_t5 ~ label("tau_Y1")*1
Y2_t1 + Y2_t2 + Y2_t3 + Y2_t4 + Y2_t5 ~ label("tau_Y2")*1
Y3_t1 + Y3_t2 + Y3_t3 + Y3_t4 + Y3_t5 ~ label("tau_Y3")*1
# Measurement error variance (time-invariant)
Y1_t1 ~~ label("merY1")*Y1_t1
Y2_t1 ~~ label("merY2")*Y2_t1
Y3_t1 ~~ label("merY3")*Y3_t1
Y1_t2 ~~ label("merY1")*Y1_t2
Y2_t2 ~~ label("merY2")*Y2_t2
Y3_t2 ~~ label("merY3")*Y3_t2
Y1_t3 ~~ label("merY1")*Y1_t3
Y2_t3 ~~ label("merY2")*Y2_t3
Y3_t3 ~~ label("merY3")*Y3_t3
Y1_t4 ~~ label("merY1")*Y1_t4
Y2_t4 ~~ label("merY2")*Y2_t4
Y3_t4 ~~ label("merY3")*Y3_t4
Y1_t5 ~~ label("merY1")*Y1_t5
Y2_t5 ~~ label("merY2")*Y2_t5
Y3_t5 ~~ label("merY3")*Y3_t5
### For the stochastic version of the model, include:
# Dynamic error variance (time-invariant)
dy2 ~~ label("derY")*dy2
dy3 ~~ label("derY")*dy3
dy4 ~~ label("derY")*dy4
dy5 ~~ label("derY")*dy5
'Step 4. Estimate the model parameters:
MI_LCS.fit <- lavaan(MI_LCS.model, data=dfwide)Click here to see the results
summary(MI_LCS.fit, standardized = T)## lavaan 0.6-8 ended normally after 42 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 52
## Number of equality constraints 38
##
## Number of observations 1980
##
## Model Test User Model:
##
## Test statistic 140.471
## Degrees of freedom 121
## P-value (Chi-square) 0.109
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 =~
## ly1 1.000 1.000 1.000
## ya =~
## dy2 1.000 0.559 0.559
## dy3 1.000 0.578 0.578
## dy4 1.000 0.589 0.589
## dy5 1.000 0.596 0.596
## dy2 =~
## ly2 1.000 0.567 0.567
## dy3 =~
## ly3 1.000 0.497 0.497
## dy4 =~
## ly4 1.000 0.452 0.452
## dy5 =~
## ly5 1.000 0.422 0.422
## ly1 =~
## Y1_t1 1.000 0.815 0.879
## Y2_t1 (l_Y2) 0.846 0.004 206.928 0.000 0.690 0.871
## Y3_t1 (l_Y3) 0.743 0.005 155.817 0.000 0.606 0.742
## ly2 =~
## Y1_t2 1.000 0.914 0.901
## Y2_t2 (l_Y2) 0.846 0.004 206.928 0.000 0.774 0.893
## Y3_t2 (l_Y3) 0.743 0.005 155.817 0.000 0.679 0.779
## ly3 =~
## Y1_t3 1.000 1.009 0.916
## Y2_t3 (l_Y2) 0.846 0.004 206.928 0.000 0.854 0.910
## Y3_t3 (l_Y3) 0.743 0.005 155.817 0.000 0.750 0.808
## ly4 =~
## Y1_t4 1.000 1.088 0.927
## Y2_t4 (l_Y2) 0.846 0.004 206.928 0.000 0.921 0.921
## Y3_t4 (l_Y3) 0.743 0.005 155.817 0.000 0.809 0.828
## ly5 =~
## Y1_t5 1.000 1.152 0.934
## Y2_t5 (l_Y2) 0.846 0.004 206.928 0.000 0.975 0.929
## Y3_t5 (l_Y3) 0.743 0.005 155.817 0.000 0.856 0.842
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ly2 ~
## ly1 1.000 0.891 0.891
## ly3 ~
## ly2 1.000 0.906 0.906
## ly4 ~
## ly3 1.000 0.927 0.927
## ly5 ~
## ly4 1.000 0.945 0.945
## dy2 ~
## ly1 (beta) -0.246 0.007 -34.340 0.000 -0.387 -0.387
## dy3 ~
## ly2 (beta) -0.246 0.007 -34.340 0.000 -0.449 -0.449
## dy4 ~
## ly3 (beta) -0.246 0.007 -34.340 0.000 -0.505 -0.505
## dy5 ~
## ly4 (beta) -0.246 0.007 -34.340 0.000 -0.551 -0.551
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 ~~
## ya 0.115 0.009 13.159 0.000 0.487 0.487
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ya -0.969 0.013 -75.917 0.000 -3.342 -3.342
## .Y1_t1 (t_Y1) -0.438 0.020 -21.828 0.000 -0.438 -0.473
## .Y1_t2 (t_Y1) -0.438 0.020 -21.828 0.000 -0.438 -0.431
## .Y1_t3 (t_Y1) -0.438 0.020 -21.828 0.000 -0.438 -0.398
## .Y1_t4 (t_Y1) -0.438 0.020 -21.828 0.000 -0.438 -0.373
## .Y1_t5 (t_Y1) -0.438 0.020 -21.828 0.000 -0.438 -0.355
## .Y2_t1 (t_Y2) -0.383 0.017 -22.469 0.000 -0.383 -0.484
## .Y2_t2 (t_Y2) -0.383 0.017 -22.469 0.000 -0.383 -0.443
## .Y2_t3 (t_Y2) -0.383 0.017 -22.469 0.000 -0.383 -0.409
## .Y2_t4 (t_Y2) -0.383 0.017 -22.469 0.000 -0.383 -0.383
## .Y2_t5 (t_Y2) -0.383 0.017 -22.469 0.000 -0.383 -0.365
## .Y3_t1 (t_Y3) -0.346 0.016 -21.196 0.000 -0.346 -0.424
## .Y3_t2 (t_Y3) -0.346 0.016 -21.196 0.000 -0.346 -0.396
## .Y3_t3 (t_Y3) -0.346 0.016 -21.196 0.000 -0.346 -0.372
## .Y3_t4 (t_Y3) -0.346 0.016 -21.196 0.000 -0.346 -0.354
## .Y3_t5 (t_Y3) -0.346 0.016 -21.196 0.000 -0.346 -0.340
## y0 0.000 0.000 0.000
## .dy2 0.000 0.000 0.000
## .dy3 0.000 0.000 0.000
## .dy4 0.000 0.000 0.000
## .dy5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## y0 0.664 0.024 27.924 0.000 1.000 1.000
## ya 0.084 0.006 13.575 0.000 1.000 1.000
## .Y1_t1 (mrY1) 0.195 0.004 46.822 0.000 0.195 0.227
## .Y2_t1 (mrY2) 0.152 0.003 48.685 0.000 0.152 0.242
## .Y3_t1 (mrY3) 0.300 0.005 62.185 0.000 0.300 0.450
## .Y1_t2 (mrY1) 0.195 0.004 46.822 0.000 0.195 0.189
## .Y2_t2 (mrY2) 0.152 0.003 48.685 0.000 0.152 0.202
## .Y3_t2 (mrY3) 0.300 0.005 62.185 0.000 0.300 0.394
## .Y1_t3 (mrY1) 0.195 0.004 46.822 0.000 0.195 0.161
## .Y2_t3 (mrY2) 0.152 0.003 48.685 0.000 0.152 0.172
## .Y3_t3 (mrY3) 0.300 0.005 62.185 0.000 0.300 0.348
## .Y1_t4 (mrY1) 0.195 0.004 46.822 0.000 0.195 0.141
## .Y2_t4 (mrY2) 0.152 0.003 48.685 0.000 0.152 0.152
## .Y3_t4 (mrY3) 0.300 0.005 62.185 0.000 0.300 0.314
## .Y1_t5 (mrY1) 0.195 0.004 46.822 0.000 0.195 0.128
## .Y2_t5 (mrY2) 0.152 0.003 48.685 0.000 0.152 0.138
## .Y3_t5 (mrY3) 0.300 0.005 62.185 0.000 0.300 0.290
## .dy2 (derY) 0.201 0.007 29.615 0.000 0.748 0.748
## .dy3 (derY) 0.201 0.007 29.615 0.000 0.799 0.799
## .dy4 (derY) 0.201 0.007 29.615 0.000 0.831 0.831
## .dy5 (derY) 0.201 0.007 29.615 0.000 0.850 0.850
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000The Bivariate LCS model
Single indicator
Obtain the example dataset here: Download BLCSdata.txt
We will estimate the following model:
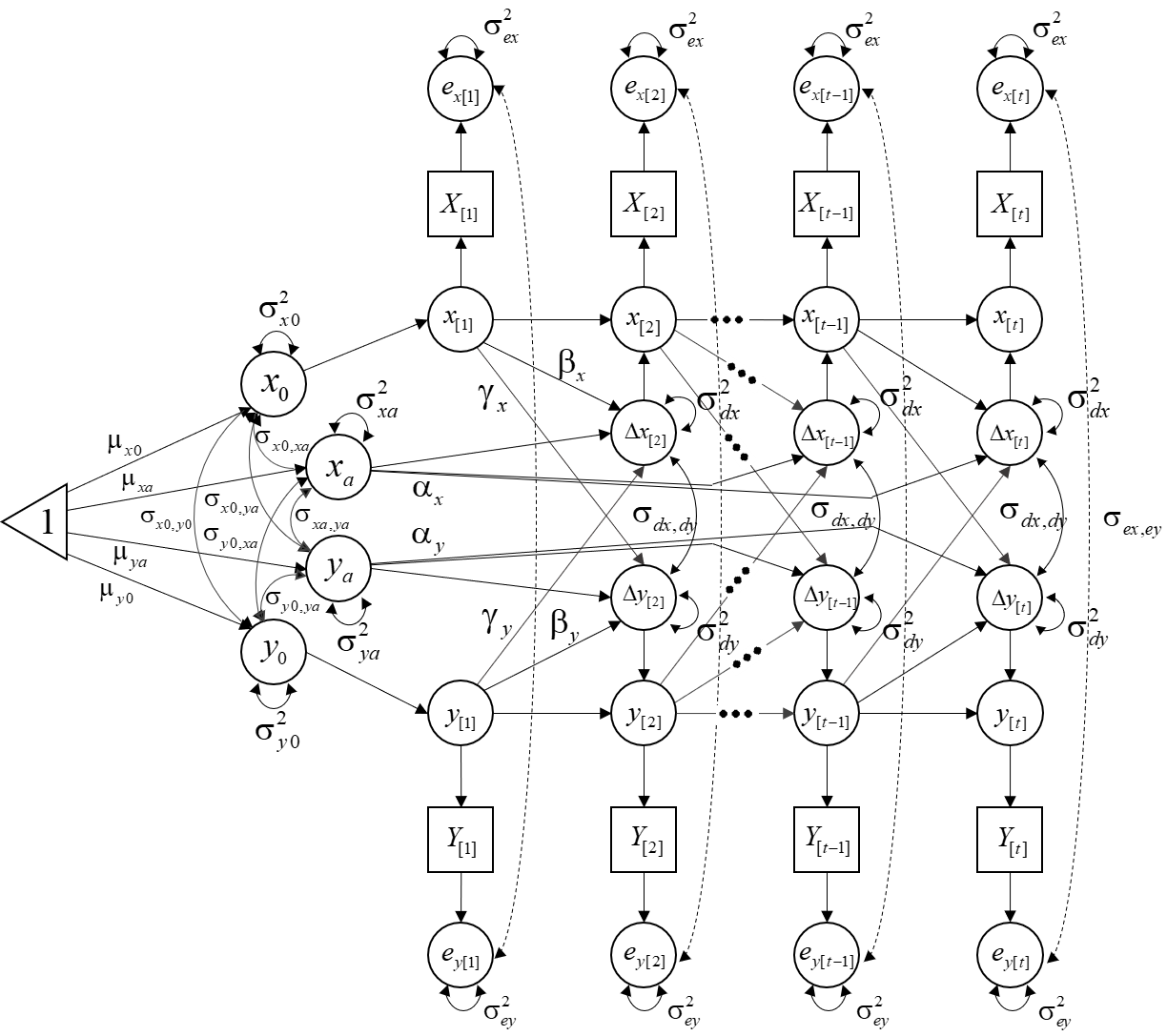
Step 1. Load the package and database:
library(lavaan)
dfwide <- read.table("BLCSdata.txt")Step 2. If necessary, name the variables in the database:
Tmax <- 5 # Number of measurement occasions
colnames(dfwide) <- c(paste0("X", 1:Tmax), paste0("Y", 1:Tmax))You can use other names for the observed variables, but make sure to use the same names when building the model.
Step 3. Build the model:
BLCS.model <- '
### Latent structure
# 1 -> Initial factor and additive component (means)
x0 + xa + y0 + ya ~ 1
# (co)variances of the initial factors and additive components
x0 ~~ x0 + xa + y0 + ya
xa ~~ xa + y0 + ya
y0 ~~ y0 + ya
ya ~~ ya
# Initial factor -> initial latent score
x0 =~ 1*lx1
y0 =~ 1*ly1
# Latent[t-1] -> Latent[t]
lx2 ~ 1*lx1
lx3 ~ 1*lx2
lx4 ~ 1*lx3
lx5 ~ 1*lx4
ly2 ~ 1*ly1
ly3 ~ 1*ly2
ly4 ~ 1*ly3
ly5 ~ 1*ly4
# Additive component -> Change
xa =~ 1*dx2 + 1*dx3 + 1*dx4 + 1*dx5
ya =~ 1*dy2 + 1*dy3 + 1*dy4 + 1*dy5
# Latent -> Change (self-feedbacks)
dx2 ~ label("beta_x")*lx1
dx3 ~ label("beta_x")*lx2
dx4 ~ label("beta_x")*lx3
dx5 ~ label("beta_x")*lx4
dy2 ~ label("beta_y")*ly1
dy3 ~ label("beta_y")*ly2
dy4 ~ label("beta_y")*ly3
dy5 ~ label("beta_y")*ly4
# Latent -> Change (couplings)
dx2 ~ label("gamma_x")*ly1
dx3 ~ label("gamma_x")*ly2
dx4 ~ label("gamma_x")*ly3
dx5 ~ label("gamma_x")*ly4
dy2 ~ label("gamma_y")*lx1
dy3 ~ label("gamma_y")*lx2
dy4 ~ label("gamma_y")*lx3
dy5 ~ label("gamma_y")*lx4
# Change -> Latent
dx2 =~ 1*lx2
dx3 =~ 1*lx3
dx4 =~ 1*lx4
dx5 =~ 1*lx5
dy2 =~ 1*ly2
dy3 =~ 1*ly3
dy4 =~ 1*ly4
dy5 =~ 1*ly5
### MEASUREMENT STRUCTURE
# Latent -> Manifest
lx1 =~ 1*X1
lx2 =~ 1*X2
lx3 =~ 1*X3
lx4 =~ 1*X4
lx5 =~ 1*X5
ly1 =~ 1*Y1
ly2 =~ 1*Y2
ly3 =~ 1*Y3
ly4 =~ 1*Y4
ly5 =~ 1*Y5
# Measurement error variances and covariances
X1 ~~ label("merX")*X1
X2 ~~ label("merX")*X2
X3 ~~ label("merX")*X3
X4 ~~ label("merX")*X4
X5 ~~ label("merX")*X5
Y1 ~~ label("merY")*Y1
Y2 ~~ label("merY")*Y2
Y3 ~~ label("merY")*Y3
Y4 ~~ label("merY")*Y4
Y5 ~~ label("merY")*Y5
X1 ~~ label("covMer")*Y1
X2 ~~ label("covMer")*Y2
X3 ~~ label("covMer")*Y3
X4 ~~ label("covMer")*Y4
X5 ~~ label("covMer")*Y5
### For the stochastic version of the model, include:
# Dynamic error variances and covariances (time-invariant constraints)
dx2 ~~ label("derX")*dx2
dx3 ~~ label("derX")*dx3
dx4 ~~ label("derX")*dx4
dx5 ~~ label("derX")*dx5
dy2 ~~ label("derY")*dy2
dy3 ~~ label("derY")*dy3
dy4 ~~ label("derY")*dy4
dy5 ~~ label("derY")*dy5
dx2 ~~ label("covDer")*dy2
dx3 ~~ label("covDer")*dy3
dx4 ~~ label("covDer")*dy4
dx5 ~~ label("covDer")*dy5
'Step 4. Estimate the model parameters:
BLCS.fit <- lavaan(BLCS.model, data=dfwide)Click here to see the results
summary(BLCS.fit, standardized = T)## lavaan 0.6-8 ended normally after 78 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 57
## Number of equality constraints 33
##
## Number of observations 1980
##
## Model Test User Model:
##
## Test statistic 29.979
## Degrees of freedom 41
## P-value (Chi-square) 0.898
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 =~
## lx1 1.000 1.000 1.000
## y0 =~
## ly1 1.000 1.000 1.000
## xa =~
## dx2 1.000 0.739 0.739
## dx3 1.000 0.469 0.469
## dx4 1.000 0.398 0.398
## dx5 1.000 0.387 0.387
## ya =~
## dy2 1.000 0.807 0.807
## dy3 1.000 0.794 0.794
## dy4 1.000 0.625 0.625
## dy5 1.000 0.543 0.543
## dx2 =~
## lx2 1.000 0.630 0.630
## dx3 =~
## lx3 1.000 0.594 0.594
## dx4 =~
## lx4 1.000 0.447 0.447
## dx5 =~
## lx5 1.000 0.332 0.332
## dy2 =~
## ly2 1.000 0.829 0.829
## dy3 =~
## ly3 1.000 0.891 0.891
## dy4 =~
## ly4 1.000 1.051 1.051
## dy5 =~
## ly5 1.000 0.779 0.779
## lx1 =~
## X1 1.000 0.787 0.824
## lx2 =~
## X2 1.000 1.048 0.889
## lx3 =~
## X3 1.000 1.752 0.956
## lx4 =~
## X4 1.000 2.746 0.981
## lx5 =~
## X5 1.000 3.802 0.990
## ly1 =~
## Y1 1.000 0.651 0.916
## ly2 =~
## Y2 1.000 0.842 0.947
## ly3 =~
## Y3 1.000 0.796 0.941
## ly4 =~
## Y4 1.000 0.857 0.949
## ly5 =~
## Y5 1.000 1.331 0.978
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## lx2 ~
## lx1 1.000 0.751 0.751
## lx3 ~
## lx2 1.000 0.598 0.598
## lx4 ~
## lx3 1.000 0.638 0.638
## lx5 ~
## lx4 1.000 0.722 0.722
## ly2 ~
## ly1 1.000 0.774 0.774
## ly3 ~
## ly2 1.000 1.057 1.057
## ly4 ~
## ly3 1.000 0.929 0.929
## ly5 ~
## ly4 1.000 0.643 0.643
## dx2 ~
## lx1 (bt_x) 0.342 0.013 26.979 0.000 0.408 0.408
## dx3 ~
## lx2 (bt_x) 0.342 0.013 26.979 0.000 0.345 0.345
## dx4 ~
## lx3 (bt_x) 0.342 0.013 26.979 0.000 0.489 0.489
## dx5 ~
## lx4 (bt_x) 0.342 0.013 26.979 0.000 0.746 0.746
## dy2 ~
## ly1 (bt_y) -0.761 0.013 -56.621 0.000 -0.710 -0.710
## dy3 ~
## ly2 (bt_y) -0.761 0.013 -56.621 0.000 -0.903 -0.903
## dy4 ~
## ly3 (bt_y) -0.761 0.013 -56.621 0.000 -0.672 -0.672
## dy5 ~
## ly4 (bt_y) -0.761 0.013 -56.621 0.000 -0.628 -0.628
## dx2 ~
## ly1 (gmm_x) 0.654 0.021 31.833 0.000 0.645 0.645
## dx3 ~
## ly2 (gmm_x) 0.654 0.021 31.833 0.000 0.529 0.529
## dx4 ~
## ly3 (gmm_x) 0.654 0.021 31.833 0.000 0.424 0.424
## dx5 ~
## ly4 (gmm_x) 0.654 0.021 31.833 0.000 0.444 0.444
## dy2 ~
## lx1 (gmm_y) -0.549 0.009 -63.227 0.000 -0.620 -0.620
## dy3 ~
## lx2 (gmm_y) -0.549 0.009 -63.227 0.000 -0.812 -0.812
## dy4 ~
## lx3 (gmm_y) -0.549 0.009 -63.227 0.000 -1.069 -1.069
## dy5 ~
## lx4 (gmm_y) -0.549 0.009 -63.227 0.000 -1.453 -1.453
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 ~~
## xa -0.103 0.013 -7.745 0.000 -0.269 -0.269
## y0 -0.133 0.015 -8.808 0.000 -0.259 -0.259
## ya 0.128 0.014 8.869 0.000 0.288 0.288
## y0 ~~
## xa -0.105 0.011 -9.562 0.000 -0.332 -0.332
## xa ~~
## ya 0.086 0.015 5.734 0.000 0.314 0.314
## y0 ~~
## ya 0.149 0.011 13.101 0.000 0.406 0.406
## .X1 ~~
## .Y1 (cvMr) 0.006 0.007 0.880 0.379 0.006 0.038
## .X2 ~~
## .Y2 (cvMr) 0.006 0.007 0.880 0.379 0.006 0.038
## .X3 ~~
## .Y3 (cvMr) 0.006 0.007 0.880 0.379 0.006 0.038
## .X4 ~~
## .Y4 (cvMr) 0.006 0.007 0.880 0.379 0.006 0.038
## .X5 ~~
## .Y5 (cvMr) 0.006 0.007 0.880 0.379 0.006 0.038
## .dx2 ~~
## .dy2 (cvDr) 0.058 0.013 4.425 0.000 0.270 0.270
## .dx3 ~~
## .dy3 (cvDr) 0.058 0.013 4.425 0.000 0.270 0.270
## .dx4 ~~
## .dy4 (cvDr) 0.058 0.013 4.425 0.000 0.270 0.270
## .dx5 ~~
## .dy5 (cvDr) 0.058 0.013 4.425 0.000 0.270 0.270
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 -1.061 0.021 -51.080 0.000 -1.349 -1.349
## xa -2.604 0.071 -36.520 0.000 -5.341 -5.341
## y0 3.316 0.016 207.947 0.000 5.093 5.093
## ya 2.593 0.047 54.603 0.000 4.607 4.607
## .X1 0.000 0.000 0.000
## .X2 0.000 0.000 0.000
## .X3 0.000 0.000 0.000
## .X4 0.000 0.000 0.000
## .X5 0.000 0.000 0.000
## .Y1 0.000 0.000 0.000
## .Y2 0.000 0.000 0.000
## .Y3 0.000 0.000 0.000
## .Y4 0.000 0.000 0.000
## .Y5 0.000 0.000 0.000
## .dx2 0.000 0.000 0.000
## .dx3 0.000 0.000 0.000
## .dx4 0.000 0.000 0.000
## .dx5 0.000 0.000 0.000
## .dy2 0.000 0.000 0.000
## .dy3 0.000 0.000 0.000
## .dy4 0.000 0.000 0.000
## .dy5 0.000 0.000 0.000
## .lx1 0.000 0.000 0.000
## .lx2 0.000 0.000 0.000
## .lx3 0.000 0.000 0.000
## .lx4 0.000 0.000 0.000
## .lx5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 0.619 0.025 24.868 0.000 1.000 1.000
## xa 0.238 0.015 15.655 0.000 1.000 1.000
## y0 0.424 0.019 22.178 0.000 1.000 1.000
## ya 0.317 0.021 15.068 0.000 1.000 1.000
## .X1 (merX) 0.292 0.010 28.582 0.000 0.292 0.321
## .X2 (merX) 0.292 0.010 28.582 0.000 0.292 0.210
## .X3 (merX) 0.292 0.010 28.582 0.000 0.292 0.087
## .X4 (merX) 0.292 0.010 28.582 0.000 0.292 0.037
## .X5 (merX) 0.292 0.010 28.582 0.000 0.292 0.020
## .Y1 (merY) 0.081 0.011 7.187 0.000 0.081 0.161
## .Y2 (merY) 0.081 0.011 7.187 0.000 0.081 0.103
## .Y3 (merY) 0.081 0.011 7.187 0.000 0.081 0.114
## .Y4 (merY) 0.081 0.011 7.187 0.000 0.081 0.100
## .Y5 (merY) 0.081 0.011 7.187 0.000 0.081 0.044
## .dx2 (derX) 0.212 0.025 8.571 0.000 0.487 0.487
## .dx3 (derX) 0.212 0.025 8.571 0.000 0.196 0.196
## .dx4 (derX) 0.212 0.025 8.571 0.000 0.141 0.141
## .dx5 (derX) 0.212 0.025 8.571 0.000 0.133 0.133
## .dy2 (derY) 0.215 0.017 13.007 0.000 0.441 0.441
## .dy3 (derY) 0.215 0.017 13.007 0.000 0.427 0.427
## .dy4 (derY) 0.215 0.017 13.007 0.000 0.265 0.265
## .dy5 (derY) 0.215 0.017 13.007 0.000 0.199 0.199
## .lx1 0.000 0.000 0.000
## .lx2 0.000 0.000 0.000
## .lx3 0.000 0.000 0.000
## .lx4 0.000 0.000 0.000
## .lx5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000Multiple Indicators
Obtain the example dataset here: Download MIBLCSdata.txt
We will estimate the following model: 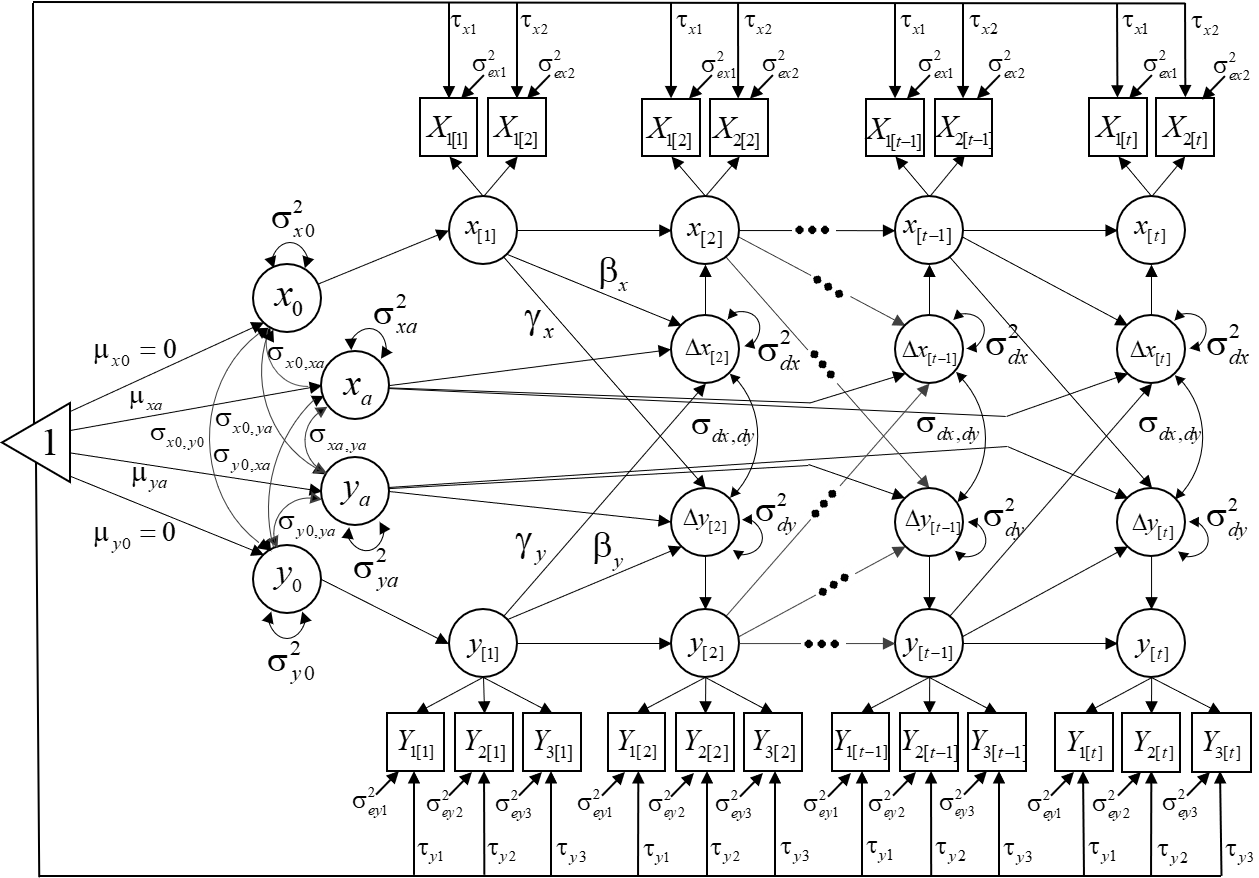
Step 1. Load the package and dataset:
library(lavaan)
dfwide <- read.table("MIBLCSdata.txt")Step 2. If necessary, name the variables in the database:
Tmax <- 5 # Number of measurement occasions
n_indicx <- 2
n_indicy <- 3
Xnames <- paste0(rep(paste0("X", 1:n_indicx, "_t"), each=Tmax), 1:Tmax)
Ynames <- paste0(rep(paste0("Y", 1:n_indicy, "_t"), each=Tmax), 1:Tmax)
colnames(dfwide) <- c(Xnames, Ynames)When building the model, we will refer to the observed variables as X1_t1, X2_t1, X1_t3… and Y1_t1, Y2_t1, Y1_t3…, where the first number identifies the indicator and the second identifies the measurement occasion.
Step 3. Build the model:
# 2. Build the model with lavaan code:
MI_BLCS.model <-'
### Latent structure
# 1 -> Additive component (means)
xa + ya ~ 1
# (co)variances of the initial factors and additive components
x0 ~~ x0 + xa + y0 + ya
xa ~~ xa + y0 + ya
y0 ~~ y0 + ya
ya ~~ ya
# Initial factor -> First latent score (t=1)
x0 =~ 1*lx1
y0 =~ 1*ly1
# Latent[t-1] -> Latent[t]
lx2 ~ 1*lx1
lx3 ~ 1*lx2
lx4 ~ 1*lx3
lx5 ~ 1*lx4
ly2 ~ 1*ly1
ly3 ~ 1*ly2
ly4 ~ 1*ly3
ly5 ~ 1*ly4
# Additive component -> Change
xa =~ 1*dx2 + 1*dx3 + 1*dx4 + 1*dx5
ya =~ 1*dy2 + 1*dy3 + 1*dy4 + 1*dy5
# Latent -> Change (self-feedbacks)
dx2 ~ label("beta_x")*lx1
dx3 ~ label("beta_x")*lx2
dx4 ~ label("beta_x")*lx3
dx5 ~ label("beta_x")*lx4
dy2 ~ label("beta_y")*ly1
dy3 ~ label("beta_y")*ly2
dy4 ~ label("beta_y")*ly3
dy5 ~ label("beta_y")*ly4
# Latent -> Change (couplings)
dx2 ~ label("gamma_x")*ly1
dx3 ~ label("gamma_x")*ly2
dx4 ~ label("gamma_x")*ly3
dx5 ~ label("gamma_x")*ly4
dy2 ~ label("gamma_y")*lx1
dy3 ~ label("gamma_y")*lx2
dy4 ~ label("gamma_y")*lx3
dy5 ~ label("gamma_y")*lx4
# Change -> Latent
dx2 =~ 1*lx2
dx3 =~ 1*lx3
dx4 =~ 1*lx4
dx5 =~ 1*lx5
dy2 =~ 1*ly2
dy3 =~ 1*ly3
dy4 =~ 1*ly4
dy5 =~ 1*ly5
### Measurement structure
# Factor loadings: Configural and weak invariance
lx1 =~ 1*X1_t1 + label("lambda_X2")*X2_t1
lx2 =~ 1*X1_t2 + label("lambda_X2")*X2_t2
lx3 =~ 1*X1_t3 + label("lambda_X2")*X2_t3
lx4 =~ 1*X1_t4 + label("lambda_X2")*X2_t4
lx5 =~ 1*X1_t5 + label("lambda_X2")*X2_t5
ly1 =~ 1*Y1_t1 + label("lambda_Y2")*Y2_t1 + label("lambda_Y3")*Y3_t1
ly2 =~ 1*Y1_t2 + label("lambda_Y2")*Y2_t2 + label("lambda_Y3")*Y3_t2
ly3 =~ 1*Y1_t3 + label("lambda_Y2")*Y2_t3 + label("lambda_Y3")*Y3_t3
ly4 =~ 1*Y1_t4 + label("lambda_Y2")*Y2_t4 + label("lambda_Y3")*Y3_t4
ly5 =~ 1*Y1_t5 + label("lambda_Y2")*Y2_t5 + label("lambda_Y3")*Y3_t5
# Intercepts of the indicators: Strong invariance
X1_t1 + X1_t2 + X1_t3 + X1_t4 + X1_t5 ~ label("tau_X1")*1
X2_t1 + X2_t2 + X2_t3 + X2_t4 + X2_t5 ~ label("tau_X2")*1
Y1_t1 + Y1_t2 + Y1_t3 + Y1_t4 + Y1_t5 ~ label("tau_Y1")*1
Y2_t1 + Y2_t2 + Y2_t3 + Y2_t4 + Y2_t5 ~ label("tau_Y2")*1
Y3_t1 + Y3_t2 + Y3_t3 + Y3_t4 + Y3_t5 ~ label("tau_Y3")*1
# Measurement error variances and covariances (time-invariant)
X1_t1 ~~ label("merX1")*X1_t1
X2_t1 ~~ label("merX2")*X2_t1
X1_t2 ~~ label("merX1")*X1_t2
X2_t2 ~~ label("merX2")*X2_t2
X1_t3 ~~ label("merX1")*X1_t3
X2_t3 ~~ label("merX2")*X2_t3
X1_t4 ~~ label("merX1")*X1_t4
X2_t4 ~~ label("merX2")*X2_t4
X1_t5 ~~ label("merX1")*X1_t5
X2_t5 ~~ label("merX2")*X2_t5
Y1_t1 ~~ label("merY1")*Y1_t1
Y2_t1 ~~ label("merY2")*Y2_t1
Y3_t1 ~~ label("merY3")*Y3_t1
Y1_t2 ~~ label("merY1")*Y1_t2
Y2_t2 ~~ label("merY2")*Y2_t2
Y3_t2 ~~ label("merY3")*Y3_t2
Y1_t3 ~~ label("merY1")*Y1_t3
Y2_t3 ~~ label("merY2")*Y2_t3
Y3_t3 ~~ label("merY3")*Y3_t3
Y1_t4 ~~ label("merY1")*Y1_t4
Y2_t4 ~~ label("merY2")*Y2_t4
Y3_t4 ~~ label("merY3")*Y3_t4
Y1_t5 ~~ label("merY1")*Y1_t5
Y2_t5 ~~ label("merY2")*Y2_t5
Y3_t5 ~~ label("merY3")*Y3_t5
### For the stochastic version of the model, include:
# Dynamic error variances and covariances (time-invariant)
dx2 ~~ label("derX")*dx2
dx3 ~~ label("derX")*dx3
dx4 ~~ label("derX")*dx4
dx5 ~~ label("derX")*dx5
dy2 ~~ label("derY")*dy2
dy3 ~~ label("derY")*dy3
dy4 ~~ label("derY")*dy4
dy5 ~~ label("derY")*dy5
dx2 ~~ label("covDer")*dy2
dx3 ~~ label("covDer")*dy3
dx4 ~~ label("covDer")*dy4
dx5 ~~ label("covDer")*dy5
'Step 4. Estimate the model parameters:
MI_BLCS.fit <- lavaan(MI_BLCS.model, data=dfwide)Click here to see the results
summary(MI_BLCS.fit, standardized = T)## lavaan 0.6-8 ended normally after 143 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 105
## Number of equality constraints 73
##
## Number of observations 1980
##
## Model Test User Model:
##
## Test statistic 348.675
## Degrees of freedom 318
## P-value (Chi-square) 0.114
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 =~
## lx1 1.000 1.000 1.000
## y0 =~
## ly1 1.000 1.000 1.000
## xa =~
## dx2 1.000 0.757 0.757
## dx3 1.000 0.476 0.476
## dx4 1.000 0.395 0.395
## dx5 1.000 0.377 0.377
## ya =~
## dy2 1.000 0.893 0.893
## dy3 1.000 0.970 0.970
## dy4 1.000 0.719 0.719
## dy5 1.000 0.597 0.597
## dx2 =~
## lx2 1.000 0.625 0.625
## dx3 =~
## lx3 1.000 0.594 0.594
## dx4 =~
## lx4 1.000 0.450 0.450
## dx5 =~
## lx5 1.000 0.335 0.335
## dy2 =~
## ly2 1.000 0.823 0.823
## dy3 =~
## ly3 1.000 0.816 0.816
## dy4 =~
## ly4 1.000 1.067 1.067
## dy5 =~
## ly5 1.000 0.777 0.777
## lx1 =~
## X1_t1 1.000 0.775 0.868
## X2_t1 (l_X2) 0.900 0.002 515.168 0.000 0.698 0.877
## lx2 =~
## X1_t2 1.000 1.028 0.918
## X2_t2 (l_X2) 0.900 0.002 515.168 0.000 0.925 0.924
## lx3 =~
## X1_t3 1.000 1.719 0.968
## X2_t3 (l_X2) 0.900 0.002 515.168 0.000 1.548 0.971
## lx4 =~
## X1_t4 1.000 2.730 0.987
## X2_t4 (l_X2) 0.900 0.002 515.168 0.000 2.459 0.988
## lx5 =~
## X1_t5 1.000 3.839 0.993
## X2_t5 (l_X2) 0.900 0.002 515.168 0.000 3.457 0.994
## ly1 =~
## Y1_t1 1.000 0.620 0.781
## Y2_t1 (l_Y2) 0.850 0.002 429.174 0.000 0.527 0.858
## Y3_t1 (l_Y3) 0.747 0.002 303.087 0.000 0.463 0.648
## ly2 =~
## Y1_t2 1.000 0.786 0.846
## Y2_t2 (l_Y2) 0.850 0.002 429.174 0.000 0.668 0.904
## Y3_t2 (l_Y3) 0.747 0.002 303.087 0.000 0.587 0.734
## ly3 =~
## Y1_t3 1.000 0.730 0.827
## Y2_t3 (l_Y2) 0.850 0.002 429.174 0.000 0.621 0.891
## Y3_t3 (l_Y3) 0.747 0.002 303.087 0.000 0.545 0.708
## ly4 =~
## Y1_t4 1.000 0.753 0.835
## Y2_t4 (l_Y2) 0.850 0.002 429.174 0.000 0.640 0.897
## Y3_t4 (l_Y3) 0.747 0.002 303.087 0.000 0.563 0.719
## ly5 =~
## Y1_t5 1.000 1.245 0.929
## Y2_t5 (l_Y2) 0.850 0.002 429.174 0.000 1.059 0.958
## Y3_t5 (l_Y3) 0.747 0.002 303.087 0.000 0.930 0.863
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## lx2 ~
## lx1 1.000 0.754 0.754
## lx3 ~
## lx2 1.000 0.598 0.598
## lx4 ~
## lx3 1.000 0.630 0.630
## lx5 ~
## lx4 1.000 0.711 0.711
## ly2 ~
## ly1 1.000 0.789 0.789
## ly3 ~
## ly2 1.000 1.077 1.077
## ly4 ~
## ly3 1.000 0.969 0.969
## ly5 ~
## ly4 1.000 0.605 0.605
## dx2 ~
## lx1 (bt_x) 0.354 0.009 41.522 0.000 0.428 0.428
## dx3 ~
## lx2 (bt_x) 0.354 0.009 41.522 0.000 0.357 0.357
## dx4 ~
## lx3 (bt_x) 0.354 0.009 41.522 0.000 0.496 0.496
## dx5 ~
## lx4 (bt_x) 0.354 0.009 41.522 0.000 0.752 0.752
## dy2 ~
## ly1 (bt_y) -0.747 0.006 -118.151 0.000 -0.716 -0.716
## dy3 ~
## ly2 (bt_y) -0.747 0.006 -118.151 0.000 -0.986 -0.986
## dy4 ~
## ly3 (bt_y) -0.747 0.006 -118.151 0.000 -0.678 -0.678
## dy5 ~
## ly4 (bt_y) -0.747 0.006 -118.151 0.000 -0.581 -0.581
## dx2 ~
## ly1 (gmm_x) 0.644 0.008 76.648 0.000 0.622 0.622
## dx3 ~
## ly2 (gmm_x) 0.644 0.008 76.648 0.000 0.496 0.496
## dx4 ~
## ly3 (gmm_x) 0.644 0.008 76.648 0.000 0.383 0.383
## dx5 ~
## ly4 (gmm_x) 0.644 0.008 76.648 0.000 0.377 0.377
## dy2 ~
## lx1 (gmm_y) -0.548 0.007 -84.264 0.000 -0.657 -0.657
## dy3 ~
## lx2 (gmm_y) -0.548 0.007 -84.264 0.000 -0.947 -0.947
## dy4 ~
## lx3 (gmm_y) -0.548 0.007 -84.264 0.000 -1.174 -1.174
## dy5 ~
## lx4 (gmm_y) -0.548 0.007 -84.264 0.000 -1.547 -1.547
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 ~~
## xa -0.125 0.011 -11.356 0.000 -0.333 -0.333
## y0 -0.102 0.013 -8.065 0.000 -0.211 -0.211
## ya 0.153 0.013 12.173 0.000 0.342 0.342
## y0 ~~
## xa -0.096 0.009 -10.669 0.000 -0.319 -0.319
## xa ~~
## ya 0.094 0.011 8.214 0.000 0.335 0.335
## y0 ~~
## ya 0.139 0.010 13.742 0.000 0.388 0.388
## .dx2 ~~
## .dy2 (cvDr) 0.026 0.005 5.406 0.000 0.151 0.151
## .dx3 ~~
## .dy3 (cvDr) 0.026 0.005 5.406 0.000 0.151 0.151
## .dx4 ~~
## .dy4 (cvDr) 0.026 0.005 5.406 0.000 0.151 0.151
## .dx5 ~~
## .dy5 (cvDr) 0.026 0.005 5.406 0.000 0.151 0.151
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## xa -2.554 0.015 -169.342 0.000 -5.258 -5.258
## ya 2.558 0.016 157.926 0.000 4.430 4.430
## .X1_t1 (t_X1) -0.551 0.019 -28.650 0.000 -0.551 -0.618
## .X1_t2 (t_X1) -0.551 0.019 -28.650 0.000 -0.551 -0.493
## .X1_t3 (t_X1) -0.551 0.019 -28.650 0.000 -0.551 -0.311
## .X1_t4 (t_X1) -0.551 0.019 -28.650 0.000 -0.551 -0.199
## .X1_t5 (t_X1) -0.551 0.019 -28.650 0.000 -0.551 -0.143
## .X2_t1 (t_X2) -0.488 0.017 -28.282 0.000 -0.488 -0.613
## .X2_t2 (t_X2) -0.488 0.017 -28.282 0.000 -0.488 -0.487
## .X2_t3 (t_X2) -0.488 0.017 -28.282 0.000 -0.488 -0.306
## .X2_t4 (t_X2) -0.488 0.017 -28.282 0.000 -0.488 -0.196
## .X2_t5 (t_X2) -0.488 0.017 -28.282 0.000 -0.488 -0.140
## .Y1_t1 (t_Y1) 1.287 0.017 75.747 0.000 1.287 1.621
## .Y1_t2 (t_Y1) 1.287 0.017 75.747 0.000 1.287 1.385
## .Y1_t3 (t_Y1) 1.287 0.017 75.747 0.000 1.287 1.458
## .Y1_t4 (t_Y1) 1.287 0.017 75.747 0.000 1.287 1.427
## .Y1_t5 (t_Y1) 1.287 0.017 75.747 0.000 1.287 0.960
## .Y2_t1 (t_Y2) 1.102 0.014 81.561 0.000 1.102 1.794
## .Y2_t2 (t_Y2) 1.102 0.014 81.561 0.000 1.102 1.491
## .Y2_t3 (t_Y2) 1.102 0.014 81.561 0.000 1.102 1.582
## .Y2_t4 (t_Y2) 1.102 0.014 81.561 0.000 1.102 1.543
## .Y2_t5 (t_Y2) 1.102 0.014 81.561 0.000 1.102 0.997
## .Y3_t1 (t_Y3) 0.989 0.015 67.603 0.000 0.989 1.385
## .Y3_t2 (t_Y3) 0.989 0.015 67.603 0.000 0.989 1.236
## .Y3_t3 (t_Y3) 0.989 0.015 67.603 0.000 0.989 1.285
## .Y3_t4 (t_Y3) 0.989 0.015 67.603 0.000 0.989 1.264
## .Y3_t5 (t_Y3) 0.989 0.015 67.603 0.000 0.989 0.918
## x0 0.000 0.000 0.000
## y0 0.000 0.000 0.000
## .dx2 0.000 0.000 0.000
## .dx3 0.000 0.000 0.000
## .dx4 0.000 0.000 0.000
## .dx5 0.000 0.000 0.000
## .dy2 0.000 0.000 0.000
## .dy3 0.000 0.000 0.000
## .dy4 0.000 0.000 0.000
## .dy5 0.000 0.000 0.000
## .lx1 0.000 0.000 0.000
## .lx2 0.000 0.000 0.000
## .lx3 0.000 0.000 0.000
## .lx4 0.000 0.000 0.000
## .lx5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## x0 0.600 0.021 28.370 0.000 1.000 1.000
## xa 0.236 0.012 19.992 0.000 1.000 1.000
## y0 0.384 0.015 26.451 0.000 1.000 1.000
## ya 0.333 0.017 19.764 0.000 1.000 1.000
## .X1_t1 (mrX1) 0.196 0.004 48.706 0.000 0.196 0.246
## .X2_t1 (mrX2) 0.146 0.003 46.729 0.000 0.146 0.231
## .X1_t2 (mrX1) 0.196 0.004 48.706 0.000 0.196 0.157
## .X2_t2 (mrX2) 0.146 0.003 46.729 0.000 0.146 0.146
## .X1_t3 (mrX1) 0.196 0.004 48.706 0.000 0.196 0.062
## .X2_t3 (mrX2) 0.146 0.003 46.729 0.000 0.146 0.057
## .X1_t4 (mrX1) 0.196 0.004 48.706 0.000 0.196 0.026
## .X2_t4 (mrX2) 0.146 0.003 46.729 0.000 0.146 0.024
## .X1_t5 (mrX1) 0.196 0.004 48.706 0.000 0.196 0.013
## .X2_t5 (mrX2) 0.146 0.003 46.729 0.000 0.146 0.012
## .Y1_t1 (mrY1) 0.246 0.005 54.465 0.000 0.246 0.391
## .Y2_t1 (mrY2) 0.100 0.002 41.918 0.000 0.100 0.264
## .Y3_t1 (mrY3) 0.295 0.005 63.206 0.000 0.295 0.579
## .Y1_t2 (mrY1) 0.246 0.005 54.465 0.000 0.246 0.285
## .Y2_t2 (mrY2) 0.100 0.002 41.918 0.000 0.100 0.182
## .Y3_t2 (mrY3) 0.295 0.005 63.206 0.000 0.295 0.461
## .Y1_t3 (mrY1) 0.246 0.005 54.465 0.000 0.246 0.316
## .Y2_t3 (mrY2) 0.100 0.002 41.918 0.000 0.100 0.206
## .Y3_t3 (mrY3) 0.295 0.005 63.206 0.000 0.295 0.498
## .Y1_t4 (mrY1) 0.246 0.005 54.465 0.000 0.246 0.303
## .Y2_t4 (mrY2) 0.100 0.002 41.918 0.000 0.100 0.195
## .Y3_t4 (mrY3) 0.295 0.005 63.206 0.000 0.295 0.483
## .Y1_t5 (mrY1) 0.246 0.005 54.465 0.000 0.246 0.137
## .Y2_t5 (mrY2) 0.100 0.002 41.918 0.000 0.100 0.082
## .Y3_t5 (mrY3) 0.295 0.005 63.206 0.000 0.295 0.254
## .dx2 (derX) 0.200 0.009 21.670 0.000 0.487 0.487
## .dx3 (derX) 0.200 0.009 21.670 0.000 0.192 0.192
## .dx4 (derX) 0.200 0.009 21.670 0.000 0.133 0.133
## .dx5 (derX) 0.200 0.009 21.670 0.000 0.121 0.121
## .dy2 (derY) 0.148 0.005 29.483 0.000 0.354 0.354
## .dy3 (derY) 0.148 0.005 29.483 0.000 0.418 0.418
## .dy4 (derY) 0.148 0.005 29.483 0.000 0.229 0.229
## .dy5 (derY) 0.148 0.005 29.483 0.000 0.158 0.158
## .lx1 0.000 0.000 0.000
## .lx2 0.000 0.000 0.000
## .lx3 0.000 0.000 0.000
## .lx4 0.000 0.000 0.000
## .lx5 0.000 0.000 0.000
## .ly1 0.000 0.000 0.000
## .ly2 0.000 0.000 0.000
## .ly3 0.000 0.000 0.000
## .ly4 0.000 0.000 0.000
## .ly5 0.000 0.000 0.000